Dihedral Group

Definition

A dihedral group is the group of symmetries of a regular polygon, including rotations and reflections.

Specifically, a mapping is in the group if it is a distance preserving map between the vertices.

\(D_{n}\) is the notation used for the dihedral group which contains \(n\) mappings. Note that this notation is not standardised, and sometimes \(D_{n}\) is used to mean the dihedral group which comes about from an \(n\) sided regular polygon. As such, one must take care when using such notation to be explicit.

In MATH3711 the \(D_n\) is the symmetries of an \(n\) sided polygon. In MATH5735 the opposite choice is made.

Generators

Theorem

The dihedral group of a \(n\) sided regular polygon is generated by \(\langle \sigma, \tau \rangle\) where:

\[ \sigma = \begin{bmatrix} \cos(\frac{2\pi}{n}) & -\sin(\frac{2\pi}{n}) \\ \sin(\frac{2\pi}{n}) & \cos(\frac{2\pi}{n}) \\ \end{bmatrix} \quad \text{and} \quad \tau = \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix}\]

and is explicitly \(\{\mathrm{id}, \sigma, \sigma^2, \dots, \sigma^{n - 1}, \tau, \sigma\tau, \dots, \sigma^{n - 1}\tau\}\).

First, let's develop an intuition for what exactly this claim is. The matrix \(\sigma\) is a rotation matrix around the origin by an angle of \(\frac{2\pi}{n}\), and hence has order \(n\). The matrix \(\tau\) is a reflection about the \(x\) axis, and is of order \(2\). Both of these facts are easy to see by their geometric interpretation, but can also be verified by computing powers.

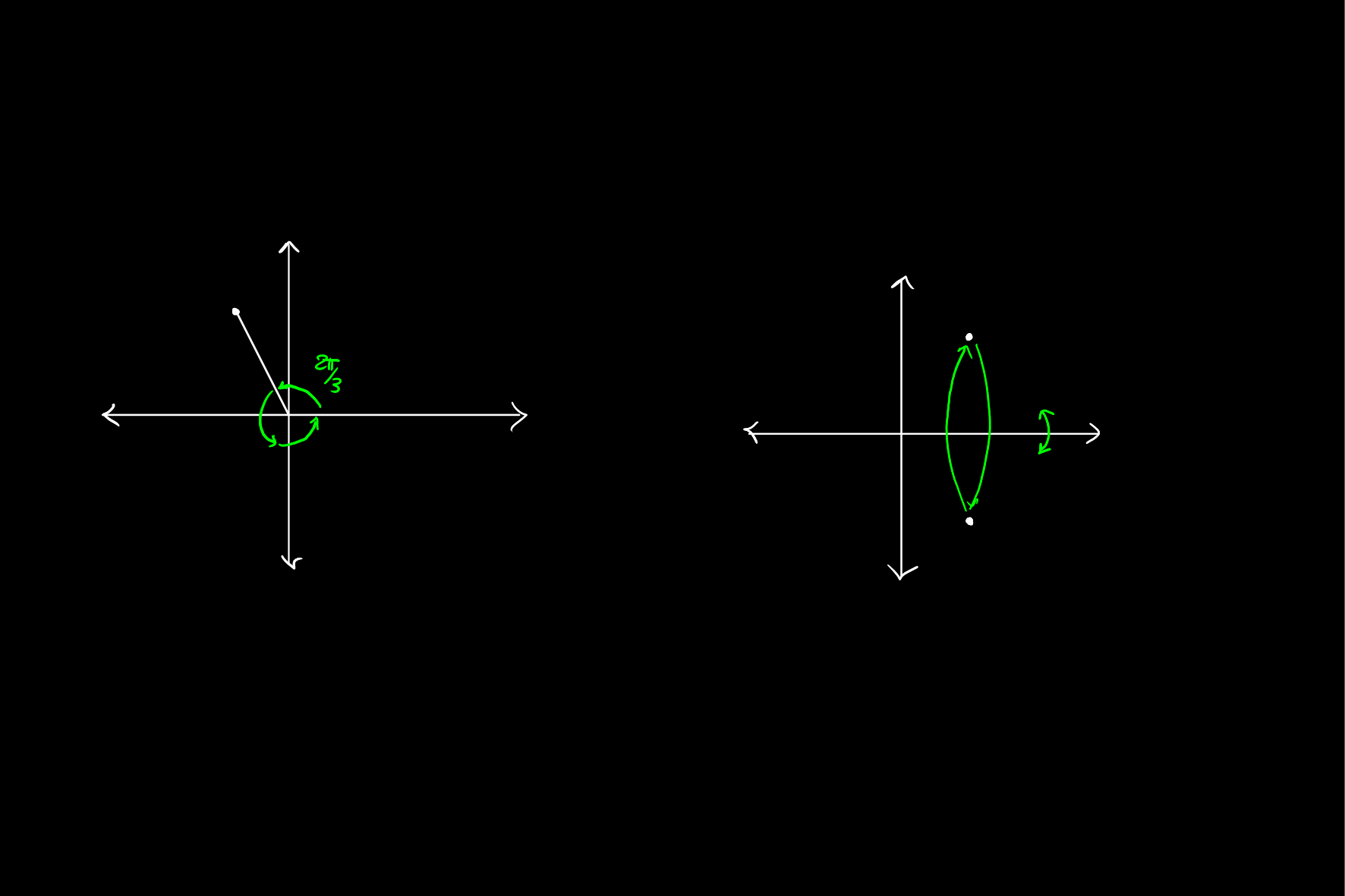
Another useful fact we will use in proving this fact is that:

\[ \tau \sigma \tau = \sigma^{-1}.\]

Again, this can be verified by matrix multiplication, but is easy to see when intuiting that all is being done is flipping the shape, rotating it, and then flipping back around, which is the same as just rotating in the opposite direction.

From this, we have that \(\tau\sigma = \sigma^{-1}\tau\) since \(\tau\) is self inverse. Furthermore, we have:

\[ \begin{align*} \tau \sigma^{i} &= \tau \underbrace{\sigma \sigma \dots \sigma}_i \\ &= \sigma^{-1} \tau \underbrace{\sigma \sigma \dots \sigma}_{i - 1} \\ &= \sigma^{-2} \tau \underbrace{\sigma \sigma \dots \sigma}_{i - 2} \\ &= \sigma^{-i} \tau \\ \end{align*}\]

Now, we can use these results to show the exact form of all elements of this group.

Specifically, consider an arbitrary combination of \(\tau\), \(\sigma\) and their inverses and powers:

\[ \sigma^{i_1} \tau^{i_2} \dots \sigma^{i_k} \tau^{i_k}.\]

Since \(\tau\) is order \(2\), we can reduce all powers of \(\tau\) to \(1\) or \(0\) and then combine adjacent powers of \(\sigma\) if \(0\), leaving an expression of the form:

\[ \sigma^{j_1} \tau \dots \sigma^{j_k} \tau.\]

Then we can use \(\tau \sigma^{i} = \sigma^{-i} \tau\) to commute the \(\tau\) terms to the right and reduce the power in much the same way, leaving something of the form \(\sigma^{l}\tau\).

Since \(\sigma\) has order \(n\), and the powers up to order in group are distinct, we can express this term with a power from \(0\) to \(n - 1\) inclusive.

Showing that these elements are distinct is just a matter of matrix multiplication.

The fact that this is equal to the group of symmetries of an \(n\) sided polygon follows from the fact that any isometry is a combination of a translation and an orthogonal matrix, and the set of orthogonal matrices consists of rotations and reflections.

Example: Equilateral Triangle

The group of distance preserving mappings of an equilateral triangle includes rotations about the axis through each of the three vertices, and two rotations about the centre point, along with the identity.

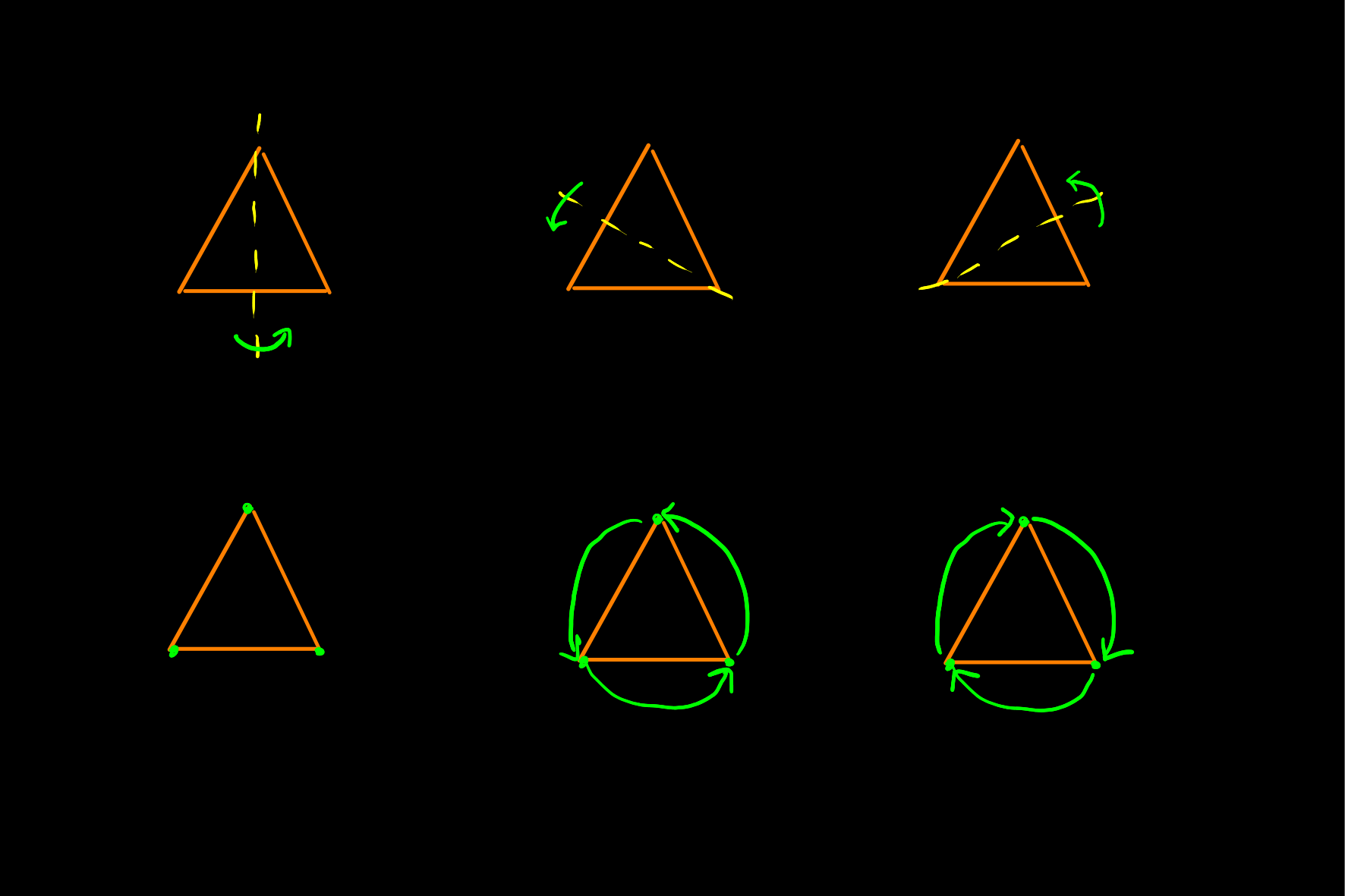
This group is \(D_{6}\), the dihedral group of order 6.